Composition of Relations
Let A, B and C be the three sets, and let R be a relation from A to B and let S be a relation from B to C. That is, R is a subset of A x B and S is a subset of B x C. Then R and S give rise to a relation from A to C denoted by R⚬S and defined by
a(R⚬S)c i.e. (a, c) ∈ R⚬S if for some b ∈ B, we have (a, b) ∈ R and (b, c) ∈ S
R⚬S = {(a, c) : there exists b ∈ B for which (a, b) ∈ R and (b, c) ∈ S}
This relation (R⚬S) is known as composition of R and S, and is sometimes simply denoted as RS.
Consider a relation R on a set A i.e. a, b ∈ A and (a, b) ∈ R. Then R⚬R, the composition of R with itself is always defined, and R⚬R is sometimes denoted by R2. Similarly, R3 = R2⚬R = R⚬R⚬R, and so on. Thus Rn is defined for all positive n.
Example :
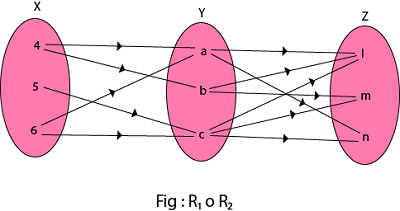
Let X = {4, 5, 6}, Y = {a, b, c} and Z = {l, m, n}. R1 = {(4, a), (4, b), (5, c), (6, a), (6, c)} is a relation from X to Y and
R2 = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)} is a relation from Y to Z.
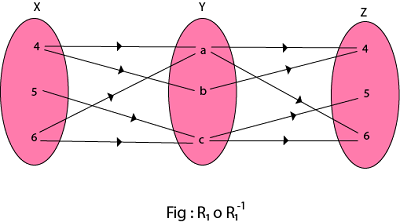
Find the composition of relation (i) R1⚬R2 (ii) R1⚬(R1)-1.
- The composition relation of R1⚬R2 is shown asR1⚬R2 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)}
- The composition relation of R1⚬(R1)-1 is shown asR1⚬(R1)-1 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)}
Composition of Relations and Matrices
There is an another way of finding R⚬S. Let MR and MS denotes the matrix representations of the relations R and S respectively. Multiplying MR and MS, we obtain the matrix representation of R⚬S. The non-zero entries in this matrix tells us which elements are related by R⚬S.
Example :
Let a set P = {2, 3, 4, 5}. Consider the relations R and S on P defined by
R = {(2, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 3)}
S = {(2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 3), (4, 5), (5, 2), (5, 5)}.
Find (i) R⚬S (ii) R⚬R (iii) S⚬R
The matrices of the relation R and S are shown as
- To obtain the composition of relation R and S, multiplying matrix MR with matrix MS asHence, the composition R⚬S of the relation R and S is
R⚬S = {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (4, 2), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)} - Now, multiplying matrix MR with itself asHence, the composition R⚬R of the relation R and S is
R⚬R = {(2, 2), (3, 2), (3, 3), (3, 4), (4, 2), (4, 5), (5, 2), (5, 3), (5, 5)} - Now, multiplying the matrix MS with matrix MR as
Hence, the composition S⚬R of the relation R and S is
S⚬R = {(2, 4), (2, 5), (3, 3), (3, 4), (3, 5), (4, 2), (4, 4), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}
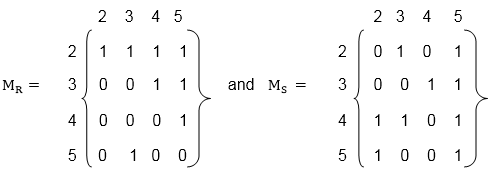
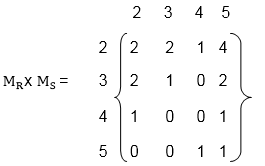
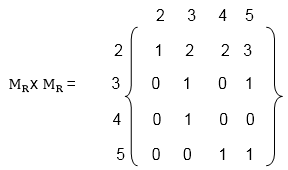
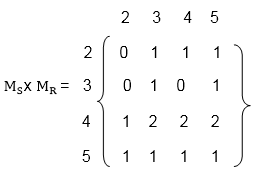
Comments
Post a Comment